System Software I
view on github- Similar Course
- Recommended Books
- Useful Commands
- Slide 1 Overview
- Slide 2 Bits&Ints
- Slide 3 Bits, Bytes and Ints
- Casting Between Signed vs. Unsigned in C
- Casting Suprises for Expression Evaluation
- Important: Ternary Operator(Conditional Operator)
- Extension
- Truncation
- Integer addition
- How to Detect Overflow in TAdd?
- Integer Multiplication
- Power-of-2 Multiply with Shift
- Unsigned Power-of-2 Divide with Shift
- Signed Power-of-2 Divide with Shift
- Difference Between Signed and Unsigned
- Slide 4 Floats
- Slide 5 Machine_Level Programmimng I: Basics
Similar Course
Recommended Books
- Computer Systems A Programmers Perspective(3rd Edition)
- The C Programming Language(EN)
- The C Programming Language(CN)
- The C Programming Language(Answer)
Useful Commands
Slide 1 Overview
Course Topics
- interact with hardware
- with system software
- linking, process, exceptionanl control flow, virtual memory
- interact with each other
- processes
- threading and synchronization
Abstraction and Reality
- limits of abstractions: especially in the presence of bugs
Reality
- Doesthis assertion succeed always?
- Data Type;
- Values of Float;
- Computer Arithmetic
- depends on function input
- performance and asymptotic complexity
- parallelism/concurrency matters
- Assembly
- Memory Matters
Slide 2 Bits&Ints
Textbook on 2.1 Information Storage
-
Every memory is identified by a unique number, known as its address, and the set of all possible addresses is known as the virtual address space.
-
The value of pointer in C - whether it points to an integer, a structure, or some other program object - is the virtual address of the first byte of some block of storage.
- The evolution of the C programming language
- Bell Labs C
- ANSI C
- ISO C90
- ISO C99
- ISO C11
- The GNU Compiler Collection(GCC) can compile programs accroding to the conventions of several different versions of the C language, based on different command-line options.
linux> gcc -std=cll prog.c - The role of pointers in C: Pointers have two aspects: its value and its type.
- value: indicates the location of some objects
- type: indicates waht kind of object(e.g., integer or floating-point number)is stored at that location.
Textbook on 2.1.1 Hexadecimal Notation
- In C, numeric starting with 0x or 0X are interpreted as being hexadecimal. The characters ‘A’ through ‘F’ may be written in either upper- or lowercase.
- Converting between binary and hexadecimal is straightforward.
- And when a value $x$ is a power of 2, that is, $x=2^n$ for some nonnegative integer n, we can readily write $x$. In binary, this will stand for as 1 followed by $n$ zeros. In hexadecimal, we can write $n$ in form of $i+4j\ (where\ 0\leq{i}\leq3)$, then we can write $x$ with a leading hex digit of 1 $(i=0)$, 2 $(i=1)$, 4 $(i=3)$, or 8 $(i=3)$, followed by $j$ hexadecimal. For example, for $x=2048=2^11=2^{3+4\times2}$, giving $i=3$ and $j=2$, which will be 0x800.
Converting Between Different Bases
-
Find the hexadecimal(base16) representation for the following number:51996
- How can we convert from decimal to hex?
- Take the value, mod it by 16 to find the quotient and remainder
- Take the remainder as the next digit(from least-significant to most)
- Repeat with quotient as the new value it reaches 0
- Therefore, for the number 51966, we can:
-
Finally, the hex should be 12,10,15,14, which is 0xCAFE
-
How to convert between
- hexidecimal
- binary
\(\mathbf{0xCAFE}\) \(1100\ 1010\ 1111\ 1110\)
Boolean Algebra
- And
- Or
- Not
- Exclusive-Or(Xor): A^B=1 when either A=1 or B=1, not both
Bits-Level Operations in C

- Bitwise complement operator~ Bitwise compliment operator is an unary operator (works on only one operand). It changes 1 to 0 and 0 to 1. It is denoted by ~.
35 = 00100011 (In Binary)
Bitwise complement Operation of 35
~ 00100011
________
11011100 = 220 (In decimal of original code)
But the value $11011100$ will be shown as -36 in C code, which is also -(35+1). This is because $11011100$ is a 2’s complement code, which can be calculated in formula:
\[-x_{w-1}\cdot2^{w-1}+\sum_{i=0}^{w-2}x_i\cdot2^i\]- Using Bit Masks to do modular arithmetic for Power of 2
unsigned int val = ... // some value to take mod
unsigned int x = ... // some power of 2
unsigned int mask = x-1;
unsigned int val_mod_x = val & mask;
For example:
x % 2 == x & 1
x % 4 == x & 3
x % 8 == x & 7
Contrast: Logistic Operations in C
- &&
- ||
- !
- Early Termination
Early Termination Example:
int x = 0;
(x++) && (x++);
printf("%d\n",x);
output x=1
int k = 0;
int d = 0;
_Bool f = ++k && d++;
printf("%d\n", k);
printf("%d\n", d);
printf("%d\n", f);
output k=1; d=1; f=0
int x = 0;
(++x) && (++x);
printf("%d\n",x);
output x=2
int x = 0;
(x++) || (x++);
printf("%d\n",x);
output x=2
Representation: Signed and Unsigned
- B2U: Binary to Unsigned
- B2T: Binary to 2’s complement
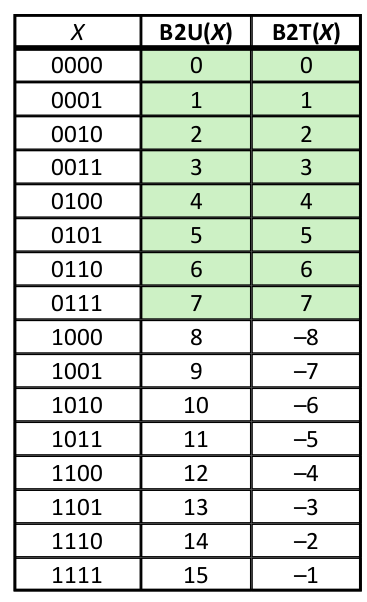
- Encoding Integers
- Unsigned: $B2U(X)=\sum_{i=0}^{w-1}x_i\cdot2^i$
- 2’ complement: $B2T(X)=-x_{w-1}\cdot2^{w-1}+\sum_{i=0}^{w-2}x_i\cdot2^i$
- Observations
- $\text{abs}(T_{Min})$ = $T_{Max}+1$
- $U_{Max} = 2\times{T_{Max}}+1$
Shift Operations
- Left Shift: $x«y$
- Right Shift: $x»y$
- For left shift operations, Arithmetic shift = Logical shift
- For right shift operations, Arithmetic shift will replicate most significant bit on the left and Logical shift will fill with 0’s on the left.
- In C programming, for signed value, C will do Arithmetic shift.
- If we use unsigned value, C will do Logical shift.

- Implement a pop_count function Use the program to get how many bits we have for a number?
# define MASK 0xF;
int main()
{
unsigned int x = -35;
int count_arr[16] = {0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4};
int count = 0;
while(x !=0){
int i = x & MASK;
count += count_arr[i];
x = x >> 4;
}
printf("%d\n", count);
return 0;
}
int pop_count(unsigned intx) {
intcount = 0;
for(; x != 0; x &= ~(x&(-x))) {
count++;
}
return count;
}
The experssion $x\&(-x)$ computes a mask with a single 1 set at least-significant position where x has a bit 1 set.
On the C code above, we will get
Output = 30
If we use signed int x = -35, the code will fall into the infinite loop, just as we said for signed value, C will do Arithmetic shift.
- In Summary
- C programming will represent a value in 2’s complement.
- For signed and unsigned value, they have different range and have different right shift.
- In computer, the length of those data type:
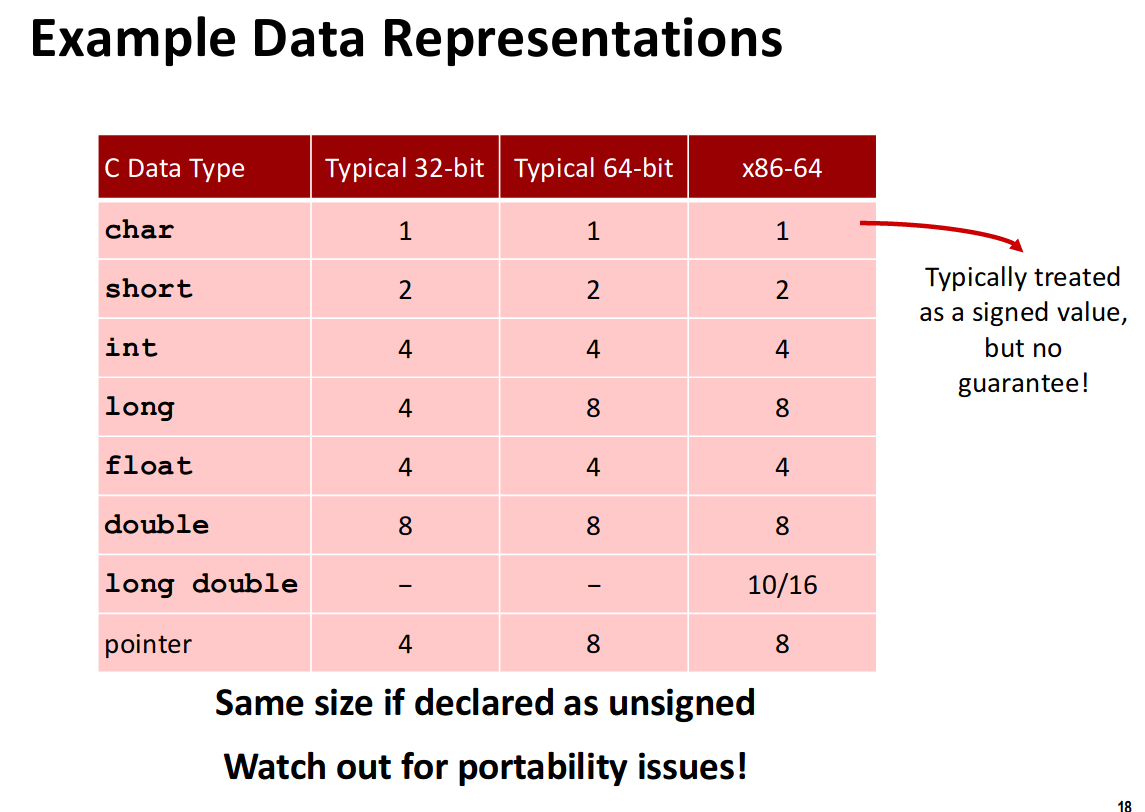
Slide 3 Bits, Bytes and Ints
Casting Between Signed vs. Unsigned in C
- Constants
- By defulat are considered to be signed integers
- Unsigned if have “U” as suffix: 0U, 42124U
- Casting
- Explicit casting between signed & unsigned same as U2T and T2U
(Tips: T stands for Two’s Complement) - Rule of Thumb: Keep bit representations and reinterpret
- Explicit casting between signed & unsigned same as U2T and T2U
short tx = -10;
short ty = -10;
unsigned short ux = 65535u;
unsigned short uy = 24u;
tx = (short) ux; //explicit cast to signed(转化为signed)
uy = (unsigned short) ty; //explicit cast to unsigned(转化为unsigned)
output: tx = -1;
uy = 65526;
What if we just use implicit way?
The answer is that the output will be same as explicit way.
tx = ux; //implicit cast to signed(转化为signed)
uy = ty; //implicit cast to unsigned(转化为unsigned)
output: tx = -1;
uy = 65526;
Tips: It is very important for us to choose right printf directives “%d” “%u”
- Printf may change the value
int x = -1;
unsigned u = 2147483648;
printf("%d, %u\n", x, x);
printf("%d, %u\n", u, u);
output: -1, 4294967295
-2147483648, 2147483648
Casting Suprises for Expression Evaluation
- If there is a mix of unsigned and signed expression, Signed values implicitly cast to unsigned (将有符号的值隐式转化为unsigned)
- Including comparison operations <, >, ==, <=, >=
- Signed and Unsigned will be evaluated based on unsigned.(If the expression contains combinations of signed and unsigned)
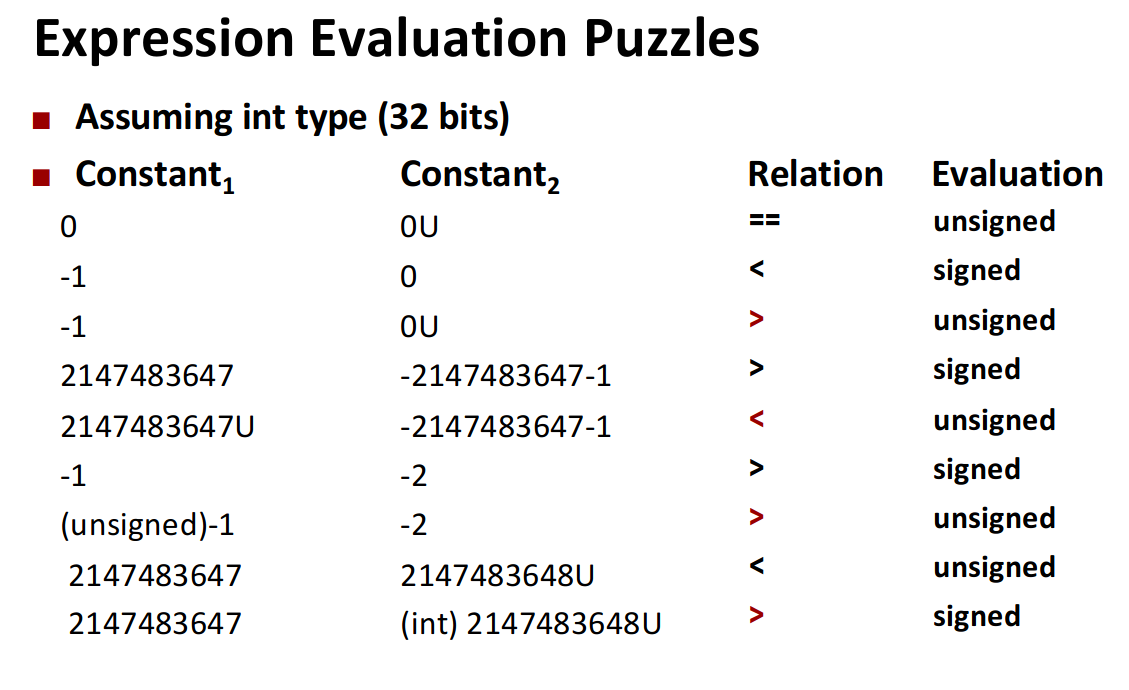
- Above them:
2147483647 (int)2147483648u Relation Evaluation
2147483647 -2147483648 > Signed
-2147483647 (int)2147483649u Relation Evaluation
1000 00....0001b
-2147483647 -2147483647 == Signed
(unsigned)-1 -2 Relation Evaluation
1111.....11b 1111...110b
4294967295 4294967294 > Unsigned
Important: Ternary Operator(Conditional Operator)
- ? :
Expression1 ? Expressoion2 : Expression3
Here, Expression1 is the condition to be evaluated. If E1 is TRUE then we will execute E2; otherwise, if E1 is FALSE, we will execute E3.
Extension
- Zero extension for unsigned type
- Given w-bit unsigned integer X
- Convert it to w+k-bit unsigned integer X’ with same value
- $X’ = 0,\cdots, 0,X_{w-1},X_{w-2},\cdots,X_{0}$
- Sign extension for Two’s complement
- Given w-bit signed integer X
- Convert it to w+k it unsigned integer X’ with same value
- $X’ = X_{w-1},\cdots, X_{w-1},X_{w-1},X_{w-2},\cdots,X_{0}$ (k copies of MSB)
- Signed Extension Preserves the value
- X is positive: easy to see that 0 bits don’t add weight
- X is negative: MSB contributed weight $-2^{w-1}$
- The $2^{nd}$ MSB and MSB contributed weight $2^{w-1}-2^{w}$
Truncation
- What is mod?
- Give the remainder after division
- Task
- Given w-bit signed integer X
- Convert it to k-bit integer X’ with same value(Maybe…)
-
Rule : Drop high-order w-k bits
- Effect:
- For Unsigned : we will do mathematical mod on X, we can do $X mod\ 2^k$
- Signed: reinterpret the bits(add $-2^{k}$ if the most significant bit is 1)
1111 1111b (255 in decimal)
if we truncate 4-bits, we will get
1111b (15 in decimal)
X' = X mod 2^k = 255 mod 2^4 = 255 mod 16 = 15
1011 1111 (-65 in decimal)
if we tr65789uncate 2-bits, we will get
11 1111 (-1 in decimal)
After we have truncated, we will get 111111, in two's complement, it is -1.
Integer addition
- Rule1: Do normal binary operations assuming enough bits, and chop off the extra bits that cannot fit.
- Rule2: The hardware does not care whether the variables are signed versus unsigned; the operations are the same for both.
unsigned int a = 6;
int b = -20;
(a+b > 6) ? puts("> 6") : puts("<= 6");
printf("%d, %u\n", a+b, a+b);
output >6;
output -14, 4294967282
-
Here we can see that unsigned value add signed value, and system just do common addition and give a binary code(unsigned).
-
How to Detect Overflow(happend) in UAdd?
- Assume w-bit operands
- If overflow, true sum $\geq{2^{w}}$, but can overflow by 1 bit only
- UAdd(u,v) = true sum mod $2^{w}=u+v-2^{w}=u+(v-2^{w})$ or $v+(u-2^{w})$
- Therefore, to detect overflow in UAdd, check if UAdd(u,v)$<$u or $<$v
- Tips: This method is just to detect whether overflow has happend
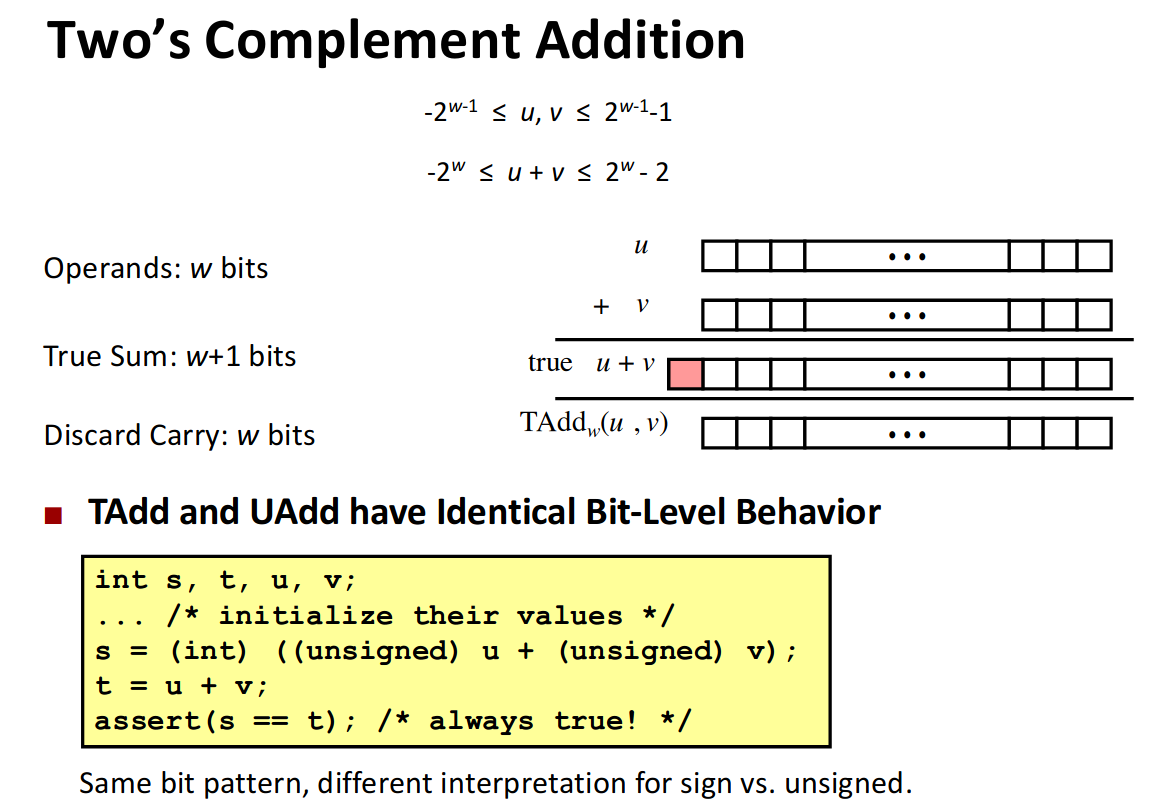
How to Detect Overflow in TAdd?
-
First we should know that only in the condition that these two numbers with the same sign (both positive or both negative). (Condition with different sign can never happen overflow.)
- Try adding two largest number together
- 0111+0111=1110(-2)
- Overflow to the MSB
- Try adding two smallest number together
- 1000+1000=10000 -> 0000(0)
- Overflow to a bit that gets truncated
- MSB must be 0
- Positive Overflow
- Adding two postive values, where $(u+v)\geq{2^{w-1}-1}$
- Wth bit contributes to true sum weight of $2^{2-1}$, but to TAdd sum $-2^{w-1}$
- TAdd sum = true sum - $2^{w}$ (negative)
- Negative Overflow
- Adding two negative values, where $(u+v)\leq{-2^{w-1}}$
- Missing the carry (w+1)th bit
- TAdd sum = true sum +$2^{w}$ (postive)
- To detect overflow in TAdd, just check if signs of input operands and out differ.
Integer Multiplication
- Rule1: Do the normal binary operations assuming enough bits, and chop off the extra bits that cannot fit.
- Rule2: The hardware does not care about whether the variables are signed versus unsigned; the operations are the same for both.
-
Just the same rule as ADDITION!
- Unsigned Multiplication in C
- Standard Multilication Function: Just ignores higher order w bits
- Implement Modular Arithmetic
- Signed Multiplication in C
- Ignores high order w bits
- Same treatment as unsigned, just reinterpret the bits
Power-of-2 Multiply with Shift
- Operation
- $u«k$ gives $u\times2^{k}$
- Both Signed and Unsigned
- Tips: Most Machines shift and add faster than multiply, compiler generates this code automatically
Example:
Q: How do you compute X*6 by using left shift?
A: 6 = 110b
Therefore, x*6 = x*(2^2+2)= x<<2 + x<<1
Unsigned Power-of-2 Divide with Shift
- Quotient of Unsigned by Power of 2
- $u»k$ gives $\lfloor{u}/{2^{k}}\rfloor$
- Uses logical shift
Signed Power-of-2 Divide with Shift
- Quotient of Unsigned by Power of 2
- $x»k$ gives $\lfloor{x}/{2^{k}}\rfloor$
- Uses arithmetic shift
Difference Between Signed and Unsigned
- Since both Signed and Unsigned will give Round Down for $x»k$, when x<0, the signed value right shift will be 1 smaller than division.
int x1 = -45;
int y1 = x1/8;
int y2 = x1>>3;
printf("%d, %d\n", y1, y2);
output: y1=-5 y2=-6
Slide 4 Floats
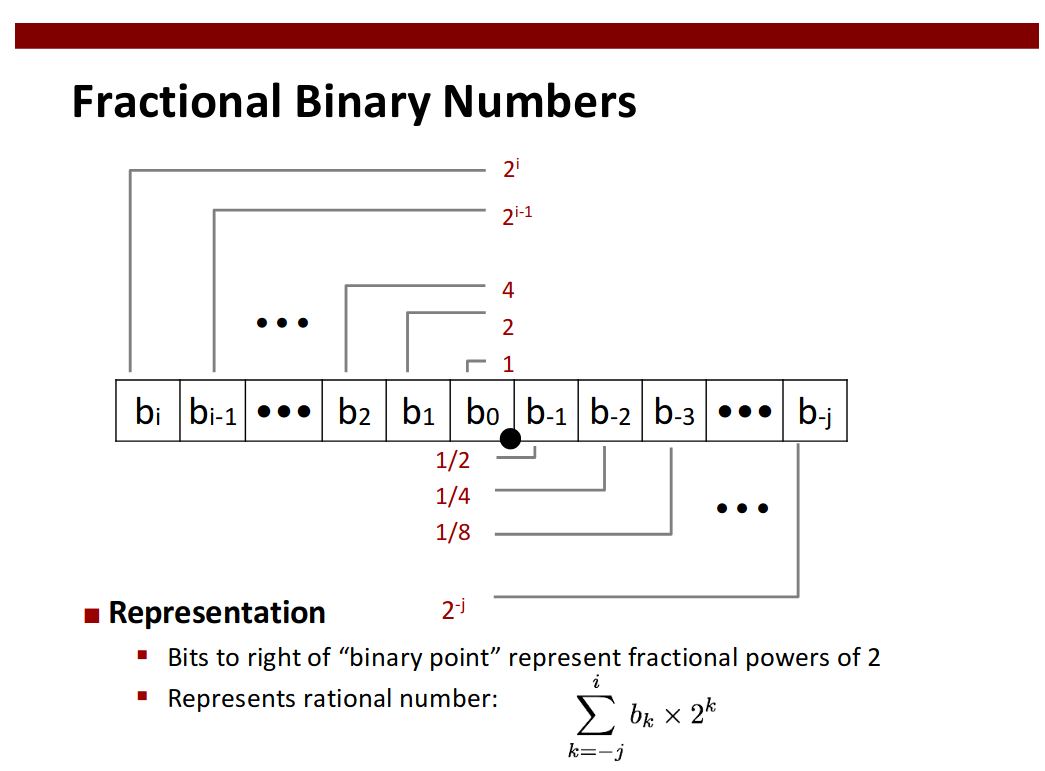
Expand Range
* Fixed Point, say fixed at xxx.x:
* range:0.1-999.9
* Floating Point:
* $x_1x_2x_3y_1$ that encodes $x\cdot10^y$
* x can range 0-999
* y can range -4-5
IEEE Floating Point
- Numerical Form:
- Encoding
- MSB s is sign bit
- exp field encodes E
- frac field encodes M
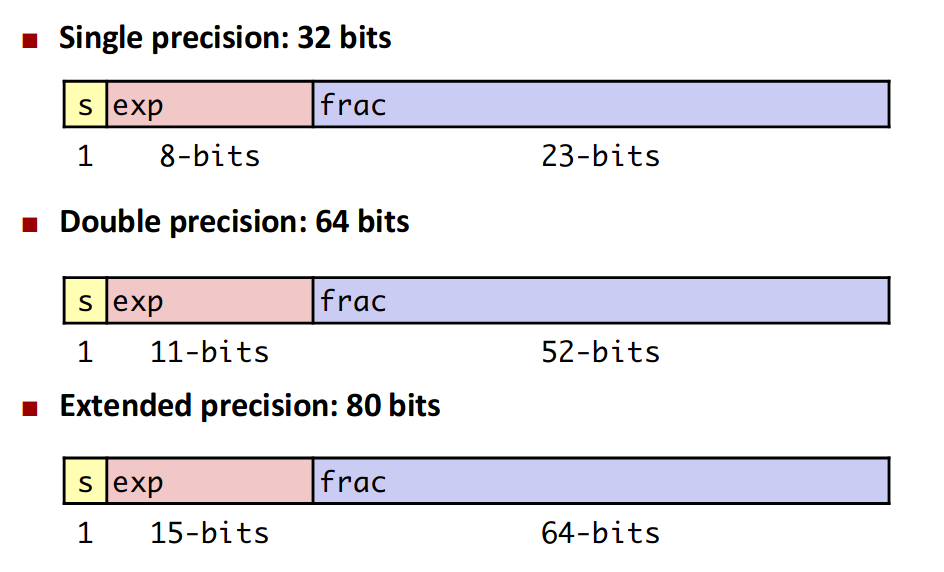
- Single Precision: 32bits
- Three Kinds of Floating Point Values
- Normalized Values
- Denormalized Values
- Sepcial exp field
- for values close to 0 or equals to 0
- Special Values
- +-infinity
- NaN
Case1: Normalized Vallues
- Condition: exp$\neq$ 000..00 and exp$\neq$ 111..11
- Mantissa coded with implied leading 1: M=1.xxxx(binary)
- $0.011\times{2^{5}}$ and $1.1\times{2^{3}}$ represent the same number, but the latter makes better use of the avaliable bits
- Range from [1, 2.0)
- Exponent coded as biased value: E = exp - bias
- bias = $2^{k-1}-1$, where k is number of exponent bits
- Single Precision: 127(exp: 1~254 E:-126 ~ 127)
- Double Precision: 1023(exp:1~2046 E: -1022~1023)
- Just as we said on above, we cannot have all O or 1 in exp bits. Therefore, we cannot give 256,255(which is -128, -127 in 2’s complement)
- bias = $2^{k-1}-1$, where k is number of exponent bits
Case2 Denormalized Values
-
This is for number 0 and numbers really close to 0)
- Condition: exp = 000…000
- Special Case: exp = 000..00, frac = 000..00
- Exponent coded as biased value: E = exp -bias
- Therefore, E will always be -126 for signle precision and -1022 for double precision
- Mantissa coded with implied leading 0: M = 0.xxxx(binary)
- Max M = 0.111..11, which is $1-\epsilon$
- TIPS: Maximum Value is little smaller than $1\times{2^{-126}}$
- Combine with E=-126 with Min M = 1.000..00. this provides smooth transition from normalized values to denormalized values
Case3 Special Values
- Condition: exp = 111…11
- Case3A: exp = 111..11, frac = 000..00 (infinity)
-
Case3B: exp = 111..11, frac$\neq$ 000…00 (NaN)
- Puzzle: What is the smallest integer cannot be represented in precisely using float in C?
- A: Key things here => integer! Since we cannot represented in float, this must be caused by overflow. With the consideration of smallest number, the best way to cause overflow is from frac portion.
- Therefore, what we get here is
S EXP frac
0 00....01( 23bits of 0 ahead 1)
Since it is overflow in integer, 1.000...01*2^24.
24 here is to make this be an integer.
Floating Point Operations and Rounding
- Multiplication

- Addition

Round
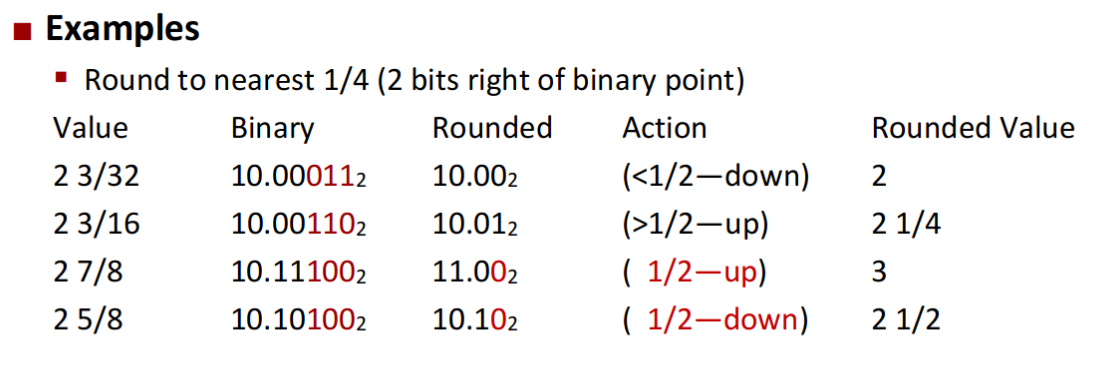
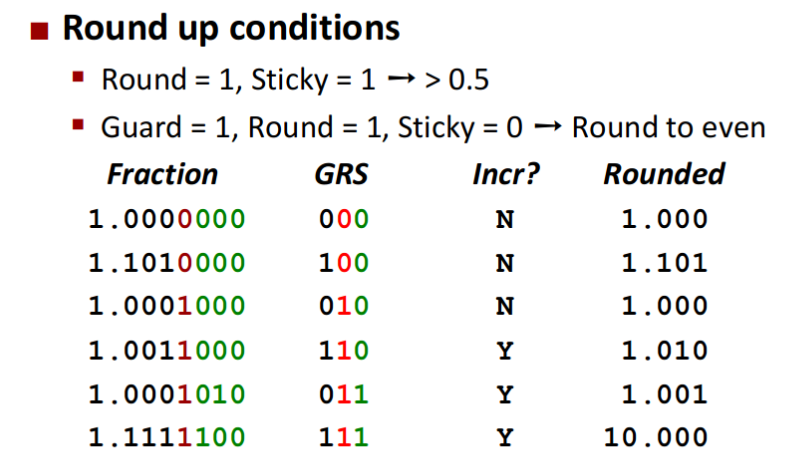
- As you can see here, rounding depends on 2 things:
- If afterwards(sticky) are larger than half, then we will increase in whatever, and vice versa.
- If afterwards(sticky) are equal to half like 10b, then we prefer to make LSB to 0(which means even).
Mathematical Properties of FP Add
- Communtative YES
- Associative NO
- …
- Additive Inverse Almost(Except for Infinities & NaN)
- …
Slide 5 Machine_Level Programmimng I: Basics
GeeksforGeeks
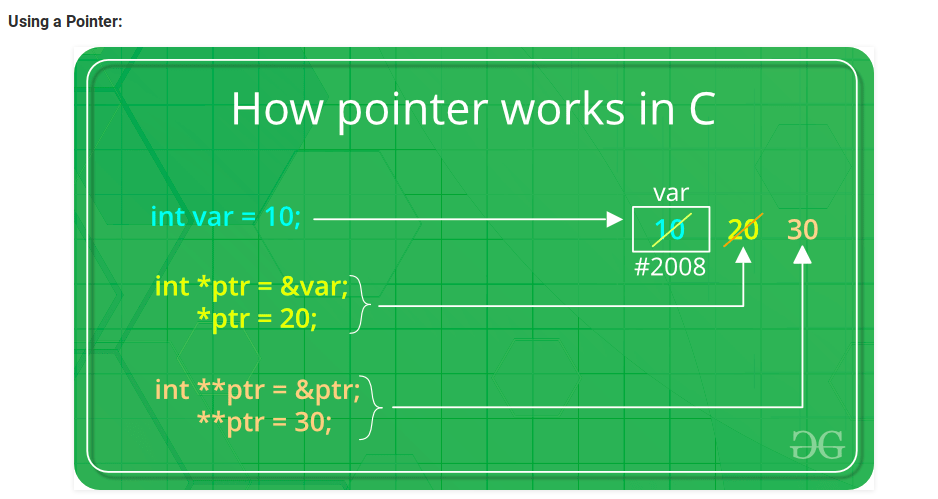
Dereference
-
Dereference Operator or Indirection Operator denoted by “ * “, is a unary operator.
- Dereference and Reference ``` & is the reference operator
- is the dereference operator ```
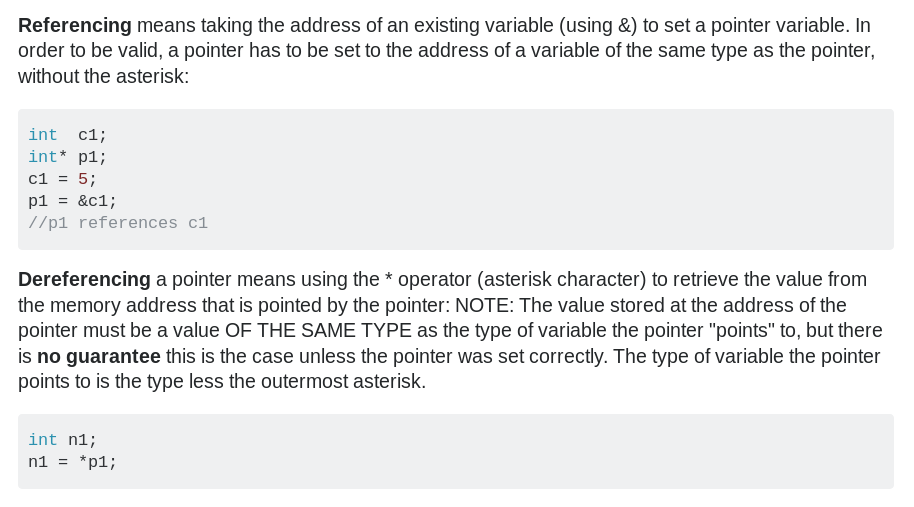
Recap Pointers in C
- The Pointer stores the address of another variable
int *p,q;
int *z;
q = 50;
// the pointer will point to q, *p is the address of q;
// *p will be the value of q
p = &q;
q = q + 1;
// this will cast the value in p to z, which means z will also point to q;
z = p;
// this will change the value of q;
*p = *p + 10;
printf("%d,%d\n", *p ,q);
printf("%d\n", *z);
output: 61,61
output: 61
int *p,q;
int *z;
q = 50;
// *p will be the value of q, but p does not point to q
*p = q;
q = q + 1;
// this will cast the value in p to z, but not pointing to q either
z = p;
// this will change the value of q;
*p = *p + 10;
printf("%d,%d\n", *p ,q);
printf("%d\n", *z);
output: 60,51
output: 60
- Swap Function
swap(&a, &b)
void swap(int *px, int *py){
// px, py points to a and b
// *px, *py return the value of a and b
int temp;
temp = *px;
*px = *py;
*py = temp;
}
- Pointers and Array
int a[10];
int *pa;
// make pa point to a[0]
pa = &a[0];
// move pointer to next element in array
// pa+1 is the address of a[1]
pa = pa + 1;
// therefore, *(pa+1) will be value of a[1]
test_a1 = *(pa);
- At here, the pointer pa=a, cause a is also a pointer in C. Therefore, the code below is equal:
// both of these codes will make pa points to array a.
pa = &a[0];
pa = a;
- In this way, we can also use *(a+i) to get the value of a[i]. And &a[i] have same meaning with a+i
*(a+1) = 0; // a[1] = 0;
pa = a+1; // pa = &a[1];