Calculus

view on github

Calculus Basic Knowledge

  • Calculus is about differentiation and integration.

1 Introduction to Limits

1.1 Limits: The Basic Use

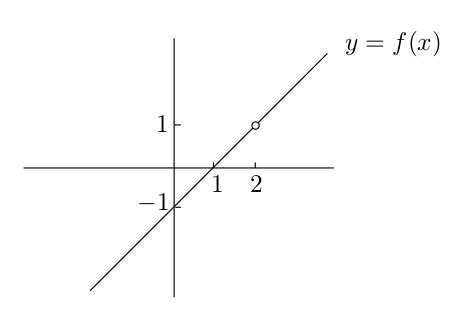
Let function $f$ have domain $\mathbb{R}\setminus$${2}$, and set $f(x)=x-1$ on this domain. Formally, you might write:

\[f(x) = x-1\ \ \text{when}\ x\neq{2}\]

And here is a question: what is $f(2)$? If you think about it, you can see that $x$ is really colse to 2, the value of $f(x)$ is really close to 1.

Anyway, let us just write

\[\lim_{x\rightarrow{2}}{f(x)=1}\]

Or another wat of writing the above statement is

\[f(x)\rightarrow{1}\ \ \text{as}\ x\rightarrow{2}\]

If you read this out loud, it should sound like “the limit, as $x$ goes to 2, of $f(x)$ is equal to 1.”

1.2 Limits: Definition

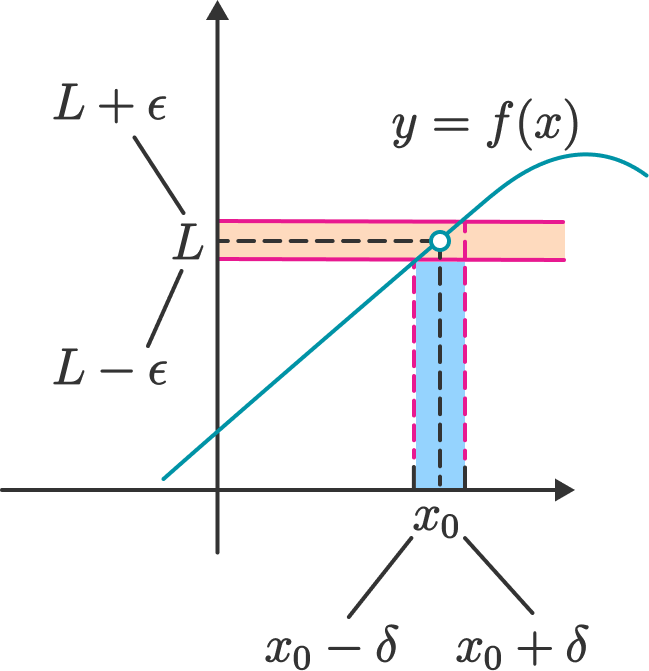
Let $f$ be a function defined on some open interval that contains the number $x_0$, except possibly at $x_0$ itself. We say the limit of $f(x)$ as $x$ approaches $x_0$ is $L$, and we write

\[\lim_{x\rightarrow{x_0}}{f(x)=L}\]

if for every $\epsilon>0$ (no matter how small $\epsilon$ is), there exists $\delta>0$ such that for all $x$

\[0<|x-x_0|<\delta\ \ \Rightarrow\ |f(x)-L|<\epsilon\]


1.3 Left-Hand[or Right-Hand] Limit: Definition

Let $f$ be a function defined on some open interval $(b,x_0)\ [\text{or\ }(x_0,b)]$. We say the left-hand [or right-hand] limit of $f(x)$ as $x$ approaches $x_0$ is $L$, and we write

\[\lim_{x\rightarrow{x_0^{-}}}{f(x)=L}\ \ \Big[\lim_{x\rightarrow{x_0^{+}}}{f(x)=L}\Big]\]

if for every $\epsilon>0$, there exists $\delta>0$ such that

\[|f(x)-L|<{\epsilon}\]

whenever

\[x_0-\delta<x<x_0\ \ [x_0<x<x_0+\delta]\]

1.4 When the Limit Does Not Exist?

  • Infinite Limit: If left-hand limit or right-hand limit DNE(Does Not Exist), like
\[\lim_{x\rightarrow{0^{+}}}{f(x)}=\lim_{x\rightarrow{0^{+}}}{\frac{1}{x}}=+\infty\]
  • Right $\neq$ Left: If left-hand limit does not equal to right-hand limit.
  • There are some interesting examples for first circumstances
    • $f(x)=\frac{1}{x}$
    • $f(x)=\frac{1}{x^2}$
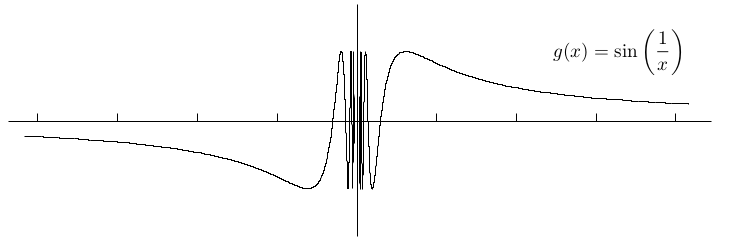
    • $f(x)=\sin(\frac{1}{x})$

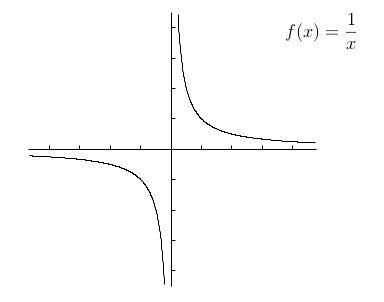
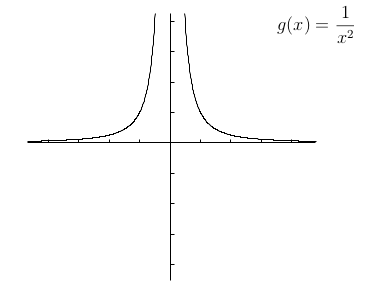
The above third graph is a real mess near $x=0$. It oscillates infinitely often between 1 and -1, faster and faster as you move from the right toward $x = 0$.

1.5 The Limit at $+\infty$ and $-\infty$

Let $f$ be a function defined on some open interval of $(a, +\infty)\ [(-\infty, a)]$. We say the limit of $f(x)$ as $x$ approaches {negative} infinity is $L$, and we write

\[\lim_{x\rightarrow{[-]\infty}}{f(x)}=L\]

if for every $\epsilon>0$, there exists $N$ such that

\[|f(x)-L|<\epsilon\]

whenever

\[x>N\ \ [x<N]\]

For example, the function $\lim_{x\rightarrow{+\infty}}{f(x)}=\lim_{x\rightarrow{+\infty}}\sin{(\frac{1}{x})}=0$

1.6 Properties of Limit

  • Property 1 (Uniqueness of Function Limits): If function $f$ has a limit as $x\rightarrow{x_0}$, then the limit is uniqueness for that.
  • Property 2 (Local Finiteness of Function Limit): If function $f$ has $\lim_{x\rightarrow{x_0}}{f(x)}=L$, then there exists $N>0$ and $\delta>0$ such that
\[0<|x-x_0|<\delta\ \ \Rightarrow\ |f(x)|\leq{N}\]
  • Property 3 (Local Guarantee of Sign for Function Limit): If function $f$ has $\lim_{x\rightarrow{x_0}}{f(x)}=L$ and $L>0$ $[L<0]$, then there exists $N>0$ and $\delta>0$ such that
\[0<|x-x_0|<\delta\ \ \Rightarrow\ f(x)>0\ [f(x)<0]\]
  • Property 4 (Relation Between Function and Sequence Limits): If limit $\lim_{x\rightarrow{x_0}}f(x)$ exists, ${x_n}$ is a sequence converges at $x_0$ ($x_n\neq{x_0}$), then corresponding function of sequence ${f(x_n)}$ must converge, and have
\[\lim_{n\rightarrow{\infty}}f(x_n)=\lim_{x\rightarrow{x_0}}f(x)\]

Proof of Property 4:
(1) Set $\lim_{x\rightarrow{x_0}}f(x)=L$, then $\forall\ {\epsilon>0}$, $\exists\ {\delta>0}$ and $0<|x-x_0|<\delta$ $\Rightarrow\ |f(x)-L|<\epsilon$
(2) Since ${x_n}$ is a sequence converges at $x_0$ ($x_n\neq{x_0}$), which equals $\lim_{n\rightarrow{\infty}}{x_n}=x_0$. It means that when $n>M$, $0<|x_n-x_0|<\delta$.
(3) As $x_n\neq{x_0}$, then if $n>M$ and $0<|x_n-x_0|<\delta$, then $|f(x_n)-L|<\epsilon$, meaning $\lim_{n\rightarrow{\infty}}f(x_n)=L$

Self Understanding of Property 4:

  • If $x$ approaches $x_0$ in common way ($x\rightarrow{x_0}$), $f(x)\rightarrow{A}$
  • If $x$ approaches $x_0$ in special way ($x_n\rightarrow{x_0}$), $f(x_n)\rightarrow{A}$

1.7 Infinite Small and Infinite Large: Definition

  • Infinite Small: If function $f$ has $\lim_{x\rightarrow{x_0}}{f(x)=0}$, then we call function $f$ is infinite small when $x$ approaches $x_0$. E.g. $\lim_{x\rightarrow{0}}{x^2}=0$, therefore, function $f$ is infinite small when $x\rightarrow{x_0}$
  • Infinite Large: Let $f$ be a function defined on some open interval that contains the number $x_0$, except possibly at $x_0$ itself. For $\forall{\ M}$, no matter how large $M$ is, there $\exists\ \delta>0$ such that
\[0<|x-x_0|<\delta\ \ \Rightarrow |f(x)|>M\]

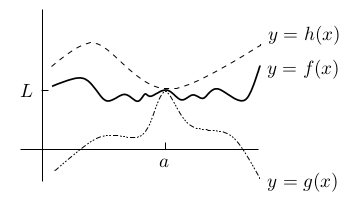
1.8 Squeeze Principle (Sandwich Principle)


1.9 An Important Limit

\[\lim_{x\rightarrow{\infty}}(1+\frac{1}{x})^{x}=e\]

1.10 Comparativeness of Infinite Small

  • If $\alpha,\beta$ are infinite small from same variable, and $\lim{\frac{\alpha}{\beta}}=0$, then we call $\beta$ is higher-order infinite small to $\alpha$. And $\lim{\frac{\alpha}{\beta}}=\infty$ for lower-order infinite small.

2 Continuity and Differentiability

2.0 Some Concepts

  • Derivative 导数
  • Derivative Function 可导函数
  • Differentiable 可微
  • Differential Function 可微函数
  • Derivative is the quotient of Differentiation for unary function(一元函数)： $f’(x)=\frac{dy}{dx}$
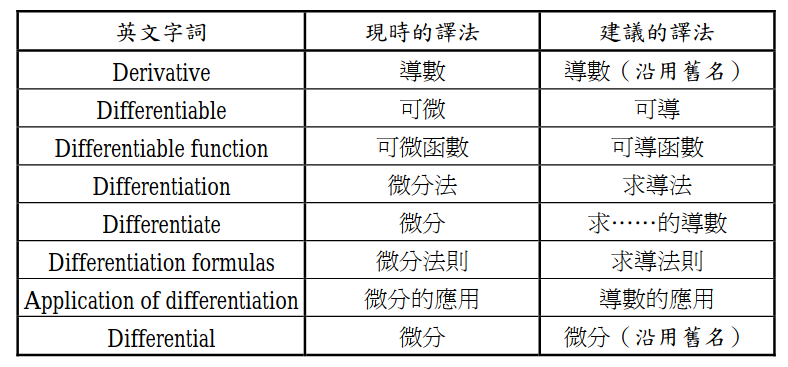
  • In English environment, there is no difference on “可导” and “可微”. Both of them are differentiable.
  • And notation $d$ stands for $\Delta$, meaning two infinitesimal $dy$ and $dx$.

2.1 Coninuity

Let $f$ be a function defined on some open interval that contains the number $x_0$, if we have $\lim_{x\rightarrow{x_0}}{f(x)}=f(x_0)$, we will declare that function $f$ is continous at point $x_0$.

2.2 Differentiability

Let $f$ be a function define on some open interval that contains the number $x_0$, we will call function $f$ is differentiate if we have limit such that

\[\lim_{\Delta{x}\rightarrow0}={\frac{f(x_0+\Delta{x})-f(x_0)}{\Delta{x}}}\]

or

\[\frac{df}{dx}\bigg\vert_{x=x_0},\frac{df(x)}{dx}\bigg\vert_{x=x_0},\ f'(x_0)\]

Some examples for not differentiate
(1) $f(x)=|x|$ when $x=0$
(2) $f(x)=|x^2-2x|$ when $x=0, x=2$

2.3 Relation Between Continuity and Differentiability

Principle: Let $f$ be a differentiable function at $x_0$, then we could assert that $f$ is continious at $x_0$. But converse proposition does not hold.

2.4 Second and Higher-Order Derivatives

  • Notation: $\frac{d^n{f}}{dx^n}\big\vert_{x=x_0},\ \ f^{(n)}(x_0)$
  • Inference: $\frac{d^n{f}}{dx^n}=\frac{d}{dx}{\frac{d^{n-1}f}{dx^{n-1}}}$

Problems:

  • 术语方面通读 chapter 6， chapter 11， 罗比达（14）
  • 积分（15，16，17，18，19）
  • 级数（22，23，24，25，26）
  • 微分方程（30）